"Ладно. пора кончать этот бардак. Давайте её закопаем"
Итак, коллеги. Товарищ
Дмитрий В. получил интересные результаты, стал мучать их в Excel и получил картинки, которые никуда не годятся. Дла начала, у нас распределение явно дискретное, а мы рисуем график как для непрерывного. Зачем точки соединять то?
Плюнем на Excel слюною, пусть в нем, товарищи, успешные менеджеры отчеты делают, нам путь в нормальный статистический пакет, поэтому только хардкор, только R.
Устанавливаем R, создаем вектор данных.
Код:
> LT<-c(rep(1,9),rep(2,267),rep(3,2843),rep(4,5450),rep(5,6564),rep(6,7044),rep(7,7518),rep(8,7071),rep(9,5620),rep(10,4016),rep(11,2545),rep(12,1494),rep(13,854),rep(14,416),rep(15,214),rep(16,122),rep(17,53),rep(18,16),rep(19,7),rep(20,2),21,22)
Функция
rep повторяет первый аргумент число раз, равное второму аргументу, поэтому для rep(1,9) имеем в результате вектор [1,1,1,1,1,1,1,1,1].
Данные берем с графика, любезно предоставленного нам.
Смотрим на результат и радуемся
Код:
> summary(LT)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.0 5.0 7.0 7.2 9.0 22.0
> length(LT)
[1] 52127
Дальше мы просто обязаны поффтыкать на картинки, иначе мы не ученые, а кот начхал.
Сказано-сделано, строим 4 графика в одном.
Код:
> old.par <- par(mfrow=c(2,2))
> hist(LT,main="Распределение букв",ylab="Число наблюдений",xlab="Число букв")
> hist(LT,freq=F,ylab="Вероятность",xlab="Число букв",main="Распределение букв")
> plot(ecdf(LT),verticals=T,main="График функции распределения")
> boxplot(LT,main="Диаграмма Ящик-с-Усами",xlab="Число букв",horizontal=T)
> par(old.par)
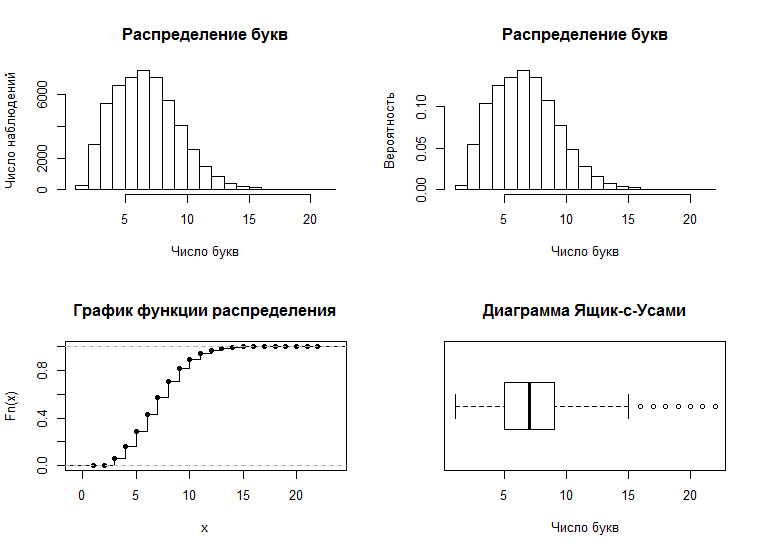
Что мы, собственно говоря видим. А видим, что распределение у нас вполне милое, да слегка несимметричное, но с кем не бывает.
Пытаемся натянуть сову на глобус. Для этого используем подгонку распределения методом максимального правдоподобия (maximum-likelihood estimation, MLE). Метод это весьма кошерен, но связан со сложными вычислениями. К счастью для нас, в R уже всё таки имеется. Достаточно подключить библиотеку MASS.
Резвимся по полной
Код:
> library(MASS)
Предупреждение
пакет ‘MASS’ был собран под R версии 2.14.2
> fitdistr(LT, "gamma")
shape rate
7.257622928 1.008025740
(0.043960087) (0.006321817)
Предупреждения
1: In dgamma(x, shape, scale, log) : созданы NaN
2: In dgamma(x, shape, scale, log) : созданы NaN
3: In dgamma(x, shape, scale, log) : созданы NaN
4: In dgamma(x, shape, scale, log) : созданы NaN
5: In dgamma(x, shape, scale, log) : созданы NaN
6: In dgamma(x, shape, scale, log) : созданы NaN
7: In dgamma(x, shape, scale, log) : созданы NaN
> fitdistr(LT, "normal")
mean sd
7.199838855 2.628803586
(0.011514015) (0.008141638)
> fitdistr(LT,"lognormal")
meanlog sdlog
1.903586097 0.385993556
(0.001690630) (0.001195456)
> fitdistr(LT, "Poisson")
lambda
7.19983886
(0.01175249)
Итак, мы что-то наподгоняли. Попробовали гамму, нормальное, логнормальное и Пуассона. В скобках, для удобства, дана ошибка параметров.
Неплохим графическим методом оценки качества подгонки распределения является график квантилей (quantile). Квантиль — это такое число, что заданная случайная величина не превышает его лишь с указанной вероятностью. Можно рассматривать квантиль как функцию вероятности Q(p), обратную функции распределения вероятностей. Если мы подогнали правильно, то точки на графике должны лежать рядом с прямой y = x. Строим четыре графика для наших распределений.
Код:
> old.par <- par(mfrow=c(2,2))
> qqplot(LT, rgamma(n = 52127, 7.257622928, 1.008025740), main = "Подгонка гамма-распределения, QQ-plot")
> abline(0, 1)
> qqplot(LT, rpois(n = 52127, 7.19983886), main = "Подгонка распределения Пуассона, QQ-plot")
> abline(0, 1)
> qqplot(LT, rnorm(n = 52127, 7.199838855,2.628803586), main = "Подгонка нормального распределения, QQ-plot")
> abline(0, 1)
> qqplot(LT, rlnorm(n = 52127, 1.903586097, 0.385993556), main = "Подгонка Логнормального распределения, QQ-plot")
> abline(0, 1)
> par(old.par)
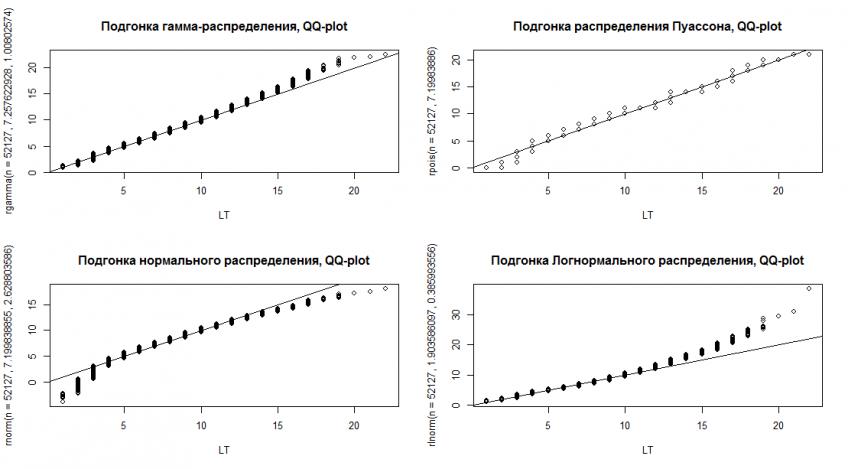
Кому как, а мне больше нравится старик Пуассон. Попробуем нарисовать график аппроксимирующих распределений.
Код:
> plot(ecdf(LT),verticals=T,main="Аппроксимация функции распределения")
> lines(0:2200/100,pgamma(0:2200/100,7.257622928, 1.008025740),col="red")
> lines(0:2200/100,ppois(0:2200/100,lambda=7.19983886),col="blue",lwd=2)
> legend(15,0.2,c("Гамма распределение","Распределение Пуассона"),col=c("red","blue"),lwd=2)
Результат

Ну, пока хватит. Коню понятно, что здесь никакая не гамма, а обычный Пуассон, причем Лямбда равна среднему числу букв в слове.
Ну, теперь сам бог велел провести тест Колмогорова-Смирнова
Код:
> ks.test(LT,rpois(0:2200/100,lambda=7.19983886))
Two-sample Kolmogorov-Smirnov test
data: LT and rpois(0:2200/100, lambda = 7.19983886)
D = 0.0261, p-value = 0.1137
alternative hypothesis: two-sided
Предупреждение
In ks.test(LT, rpois(0:2200/100, lambda = 7.19983886)) :
p-values будут примерными в присутствии повторяющихся значений
Ай, да Hogfather, хочется сказать, ай, молодец!
Бурные продолжительные аплодисменты.
А гамма ваша, кака редкая...
Код:
> ks.test(LT,rgamma(0:2200/100, 7.257622928, 1.008025740))
Two-sample Kolmogorov-Smirnov test
data: LT and rgamma(0:2200/100, 7.257622928, 1.00802574)
D = 0.1011, p-value < 2.2e-16
alternative hypothesis: two-sided
Предупреждение
In ks.test(LT, rgamma(0:2200/100, 7.257622928, 1.00802574)) :
p-values будут примерными в присутствии повторяющихся значений
Согласен на соавторство

P.S. Ну, мои маленькие девиантные друзья, если кто хочет поподробнее почитать про подгонку распределений в R, рекомендую на сон грядущий статью
"Fitting distributions with R"
P.P.S. А список наиболее распространенных распределений можно посмотреть
вот тут, в вашей любимой Википедии