"Пора кончать этот бардак. Давайте её откопаем"
Как говорится. не только методом максимального правдоподобия славен R. Ту же задачу можно попробовать решить
нелинейным методом наименьших квадратов. Для этого построим кумулятивную (интегральную) функцию распределения и попробуем подогнать понравившегося нам Пуассона. В общем, сделаем примерно то, что пытался проделать
Дмитрий В. в Excel.
Код:
> # Понеслась!
> # Строим кумулятивную функцию
> MyEcdf<-ecdf(LT)
># Делаем таблицу (фрейм) для аппроксимации
># Обратите внимание, поскольку я все взял в скобки, результат отображается сразу на экране
> (dfecdf <- data.frame(knots=knots(MyEcdf),Fn=MyEcdf(1:22)))
knots Fn
1 1 0.0001726552
2 2 0.0052947609
3 3 0.0598346346
4 4 0.1643869780
5 5 0.2903102039
6 6 0.4254417097
7 7 0.5696663917
8 8 0.7053158632
9 9 0.8131294723
10 10 0.8901720797
11 11 0.9389951465
12 12 0.9676559173
13 13 0.9840389817
14 14 0.9920194909
15 15 0.9961248489
16 16 0.9984652867
17 17 0.9994820343
18 18 0.9997889769
19 19 0.9999232643
20 20 0.9999616322
21 21 0.9999808161
22 22 1.0000000000
> # Строим модель
> mdl<-nls( Fn ~ ppois(knots,lambda), data=dfecdf,model=T)
Предупреждение
In nls(Fn ~ ppois(knots, lambda), data = dfecdf, model = T) :
Для некоторых параметров не указаны стартовые значения.
Инициализую ‘lambda’ до '1.'.
Укажите 'start' или я использую модель 'selfStart'
> # Информация о модели
> summary(mdl)
Formula: Fn ~ ppois(knots, lambda)
Parameters:
Estimate Std. Error t value Pr(>|t|)
lambda 7.16774 0.01924 372.5 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.006275 on 21 degrees of freedom
Number of iterations to convergence: 5
Achieved convergence tolerance: 3.776e-08
Посчитаем адекватность полученной модели.
Код:
> # Расчет адекватности модели
> (RSS.p <- sum(residuals(mdl)^2))
[1] 0.000826937
> (TSS <- sum((dfecdf$Fn - mean(dfecdf$Fn))^2))
[1] 2.981961
> # коэффициент детерминации
> 1 - (RSS.p/TSS)
[1] 0.9997227
Что мы имеем с гуся. А с гуся имеем чуть другую лямбду (7.16774) и коэффициент детерминации практически единицу.
Для лямбды можно посчитать доверительный интервал
Код:
> confint(mdl)
Waiting for profiling to be done...
2.5% 97.5%
7.127763 7.207781
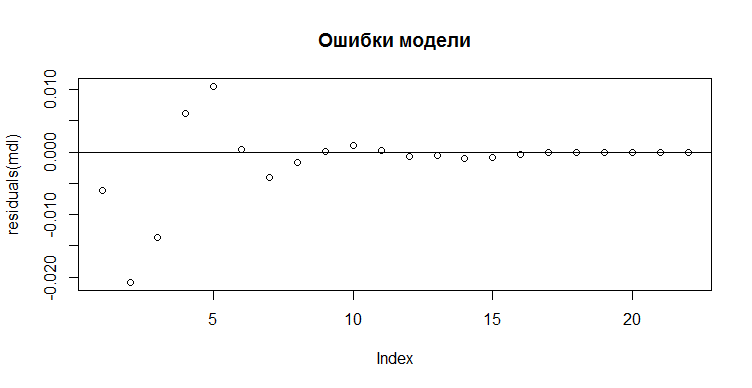
Графически ошибки модели можно изобразить вот так.
Код:
> plot(residuals(mdl),main="Ошибки модели")
> abline(0,0)