[Hogfather]

"Нет, всё-таки откопаем..."

Итак, более корректная и интересная первая подгонка, поскольку во втором случае мы просто подгоняем функцию по 22 точкам. С интересом обнаружил, что в 2012 году для R вышел более мощный пакет подгонки fitdistrplus.

Попробуем в него поиграть. Опять берем Гамму.

>#Подключаем библиотеку
>library(fitdistrplus)
># Подгоняем гамма-распределение
> XX<-fitdist(LT, "gamma")
> summary(XX)
Fitting of the distribution ' gamma ' by maximum likelihood 
Parameters : 
      estimate  Std. Error
shape 7.258422 0.043965053
rate  1.008084 0.006322175
Loglikelihood:  -122729.7   AIC:  245463.4   BIC:  245481.2 
Correlation matrix:
          shape      rate
shape 1.0000000 0.9658169
rate  0.9658169 1.0000000

Ну и Пуассона

># Подгоняем распределение Пуассона
> XY<-fitdist(LT, "pois")
> summary(XY)
Fitting of the distribution ' pois ' by maximum likelihood 
Parameters : 
       estimate Std. Error
lambda 7.199839 0.01175249
Loglikelihood:  -123149.4   AIC:  246300.8   BIC:  246309.7

Результаты совпали, но зато у нас появилось много умных буковок, которые сказочно обогатят нашу статью.

Пакет позволяет построить красивые картинки. Причем очень просто.

># Рисунок для гаммы
> plot(XX)
># Рисунок для Пуассона
> plot(XY)

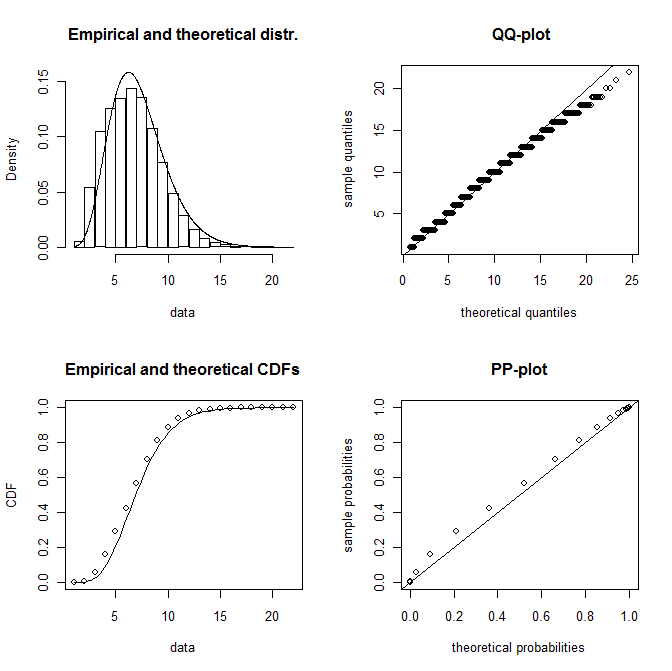
Рисунок 1 -- Подгонка гамма-распределения


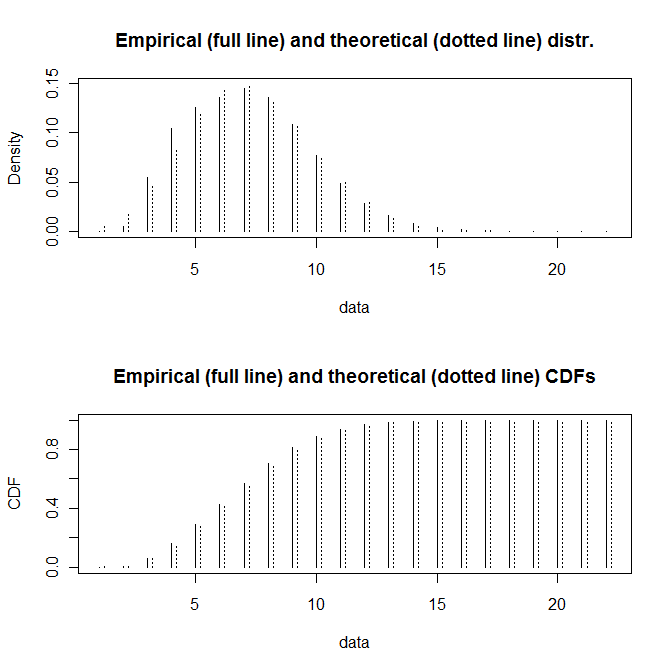
Рисунок 2 -- Подгонка распределения Пуассона

Рисунок 2 можно также получить не прибегая к построению модели.
Для распределения Пуассона с лямбдой равной средней длине слова это выглядит так:

> plotdist(LT,"pois",para=list(lambda=mean(LT)))

А можно легко и непринужденно посчитать статистические параметры и проверить гипотезы.

># Для гамма-распределения
>  gofstat(XX,print.test=TRUE)
Kolmogorov-Smirnov statistic:  0.09400709 
Kolmogorov-Smirnov test:  rejected 
   The result of this test may be too conservative as it  
   assumes that the distribution parameters are known
Cramer-von Mises statistic:  68.65376 
Cramer-von Mises test:  rejected 
Anderson-Darling statistic:  397.2767 
Anderson-Darling test:  rejected 

># Для Распределения Пуассона
> g2 <- gofstat(XY,print.test=TRUE)
Chi-squared statistic:  445.9628 
Degree of freedom of the Chi-squared distribution:  11 
Chi-squared p-value:  1.041315e-88 
> g2$chisqtable
      obscounts theocounts
<= 3  3119.0000  3749.2137
<= 4  5450.0000  4358.0510
<= 5  6564.0000  6275.4530
<= 6  7044.0000  7530.3751
<= 7  7518.0000  7745.3553
<= 8  7071.0000  6970.6637
<= 9  5620.0000  5576.4062
<= 10 4016.0000  4014.9226
<= 11 2545.0000  2627.8905
<= 12 1494.0000  1576.6990
<= 13  854.0000   873.2291
<= 14  416.0000   449.0792
> 14   416.0000   379.6615
>

Первоначальный выбор возможного распределения также осуществляется легко и непринужденно, посчитав моменты.

> descdist(LT)
summary statistics
------
min:  1   max:  22 
median:  7 
mean:  7.199839 
estimated sd:  2.628829 
estimated skewness:  0.519882 
estimated kurtosis:  3.143716

Вот такая красота.


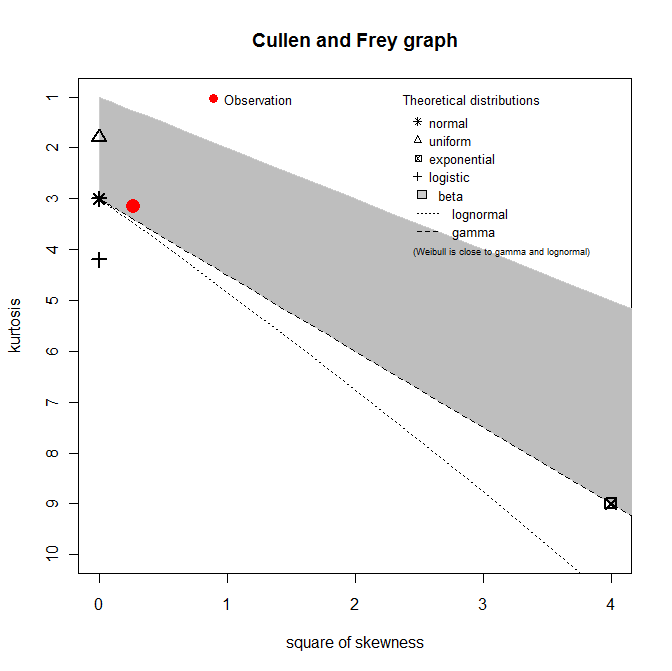Но, поскольку у нас распределение дискретное, мы нарисуем другой график.

> descdist(LT,discrete = TRUE,boot=1000)
summary statistics
------
min:  1   max:  22 
median:  7 
mean:  7.199839 
estimated sd:  2.628829 
estimated skewness:  0.519882 
estimated kurtosis:  3.143716

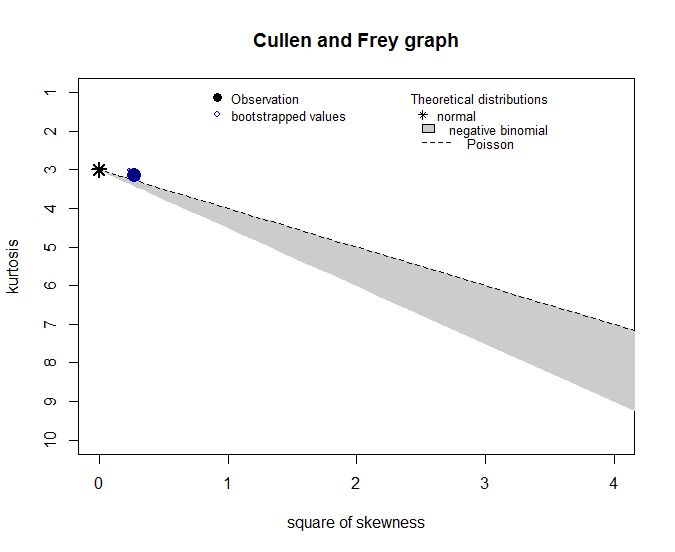Почти Пуассон, красота!

В общем, пакет мне понравился. Буду пользоваться.

P.S. Если как положено считать Хи-квадрат для дискретного распределения, то видно, что и распределение Пуассона не торт.

Еще разные распределения

> XZ<-fitdist(LT,"beta")
Ошибка в mledist(data, distname, start, fix.arg, ...) : 
  values must be in [0-1] to fit a beta distribution
> XZ<-fitdist(LT/52127,"beta")
Предупреждения
1: In dbeta(x, shape1, shape2, log) : созданы NaN
2: In dbeta(x, shape1, shape2, log) : созданы NaN
3: In dbeta(x, shape1, shape2, log) : созданы NaN
4: In dbeta(x, shape1, shape2, log) : созданы NaN
5: In dbeta(x, shape1, shape2, log) : созданы NaN
6: In dbeta(x, shape1, shape2, log) : созданы NaN
7: In dbeta(x, shape1, shape2, log) : созданы NaN
8: In dbeta(x, shape1, shape2, log) : созданы NaN
9: In dbeta(x, shape1, shape2, log) : созданы NaN
10: In dbeta(x, shape1, shape2, log) : созданы NaN
> summary(XZ)
Fitting of the distribution ' beta ' by maximum likelihood 
Parameters : 
           estimate   Std. Error
shape1     7.257806   0.01867214
shape2 52538.205482 114.78284503
Loglikelihood:  443444.6   AIC:  -886885.2   BIC:  -886867.5 
Correlation matrix:
          shape1    shape2
shape1 1.0000000 0.7921102
shape2 0.7921102 1.0000000

> gofstat(XZ,print.test=TRUE)
Kolmogorov-Smirnov statistic:  0.09402943 
Kolmogorov-Smirnov test:  rejected 
   The result of this test may be too conservative as it  
   assumes that the distribution parameters are known
Cramer-von Mises statistic:  68.67007 
Crame-von Mises test: not calculated 
Anderson-Darling statistic:  397.3218 
Anderson-Darling test: not calculated 

> XZ<-fitdist(LT,"nbinom")
Предупреждение
In dnbinom_mu(x, size, mu, log) : созданы NaN

> summary(XZ)
Fitting of the distribution ' nbinom ' by maximum likelihood 
Parameters : 
         estimate Std. Error
size 1.037875e+06 8.85828908
mu   7.199210e+00 0.01175151
Loglikelihood:  -123149.4   AIC:  246302.8   BIC:  246320.5 
Correlation matrix:
              size            mu
size  1.000000e+00 -1.325475e-06
mu   -1.325475e-06  1.000000e+00

> gofstat(XZ,print.test=TRUE)
Chi-squared statistic:  445.6481 
Degree of freedom of the Chi-squared distribution:  10 
Chi-squared p-value:  1.770972e-89 

> XZ<-fitdist(LT,"geom")
Предупреждения
1: In dgeom(x, prob, log) : созданы NaN
2: In dgeom(x, prob, log) : созданы NaN
> gofstat(XZ,print.test=TRUE)
Chi-squared statistic:  62647.84 
Degree of freedom of the Chi-squared distribution:  11 
Chi-squared p-value:  0 

> (XZ<-fitdist(LT,"weibull"))
Fitting of the distribution ' weibull ' by maximum likelihood 
Parameters:
      estimate  Std. Error
shape 2.937583 0.009692365
scale 8.075648 0.012729966

> gofstat(XZ,print.test=TRUE)
Kolmogorov-Smirnov statistic:  0.08801459 
Kolmogorov-Smirnov test:  rejected 
   The result of this test may be too conservative as it  
   assumes that the distribution parameters are known
Cramer-von Mises statistic:  65.77123 
Cramer-von Mises test:  rejected 
Anderson-Darling statistic:  400.9466 
Anderson-Darling test:  rejected

Добавлено через 3 часа 40 минут

Сообщение от Hogfather

Ну, теперь сам бог велел провести тест Колмогорова-Смирнова

Сообщение от Вляпалась...

Чистенько, аккуратненько, корректненько.

Если бы. Наврал ведь, а хоть бы кто поправил. Для дискретного распределения тест Колмогорова-Смирнова не применяется, так как его предельные распределения получены в предположении о непрерывности и случайных величин, и их законов распределения . Поэтому только Хи-квадрат, либо через метод обратного преобразования.

В общем, Колмогорова-Смирнова в данном случае не трогаем. Хотя, красивый результат вышел. То-то мне он подозрительным показался.