|
Platinum Member
Регистрация: 22.07.2010
Адрес: Санкт-Петербург
Сообщений: 3,304
|
 Множественная линейная регрессия
Множественная линейная регрессия
Наши постоянные читатели спрашивают
Цитата:
Будет замечательно, если Вы рассмотрите данную задачу как пример.
Задача: получить зависимость z(x,y)
Исходные данные:
x <- c(75, 75, 75, 75, 100, 125, 125, 150, 150, 175, 175, 200, 200, 225, 250, 250, 250, 275, 300, 300, 300, 300)
y <- c(375, 625, 1000, 1500, 500, 375, 1125, 750, 1250, 825, 1500, 375, 1000, 1125, 750, 1250, 1500, 1375, 375, 825, 1500, 1250)
z <- c(1.452, 3.705, 18.857, 50.434, 1.956, 2.272, 40.306, 3.368, 47.686, 4.464, 55.63, 2.611, 9.077, 15.304, 7.559, 27.257, 60.174, 35.965, 3.355, 22.491, 38.036, 54.237)
|
Ну, что ж. Начнем. Загоняем данные в R и делаем Data Frame (таблицу)
Код:
> x <- c(75, 75, 75, 75, 100, 125, 125, 150, 150, 175, 175, 200, 200, 225, 250, 250, 250, 275, 300, 300, 300, 300)
> y <- c(375, 625, 1000, 1500, 500, 375, 1125, 750, 1250, 825, 1500, 375, 1000, 1125, 750, 1250, 1500, 1375, 375, 825, 1500, 1250)
> z <- c(1.452, 3.705, 18.857, 50.434, 1.956, 2.272, 40.306, 3.368, 47.686, 4.464, 55.63, 2.611, 9.077, 15.304, 7.559, 27.257, 60.174, 35.965, 3.355, 22.491, 38.036, 54.237)
> myData<-data.frame(x,y,z)
Вторым нашим шагом будет полюбоваться на наши данные, чтобы увидеть зависимость, используя корреляционную матрицу.
Код:
> library(lattice)
> splom(~myData[,c("x","y","z")],cex.labels=1.2,varnames=c("x","y","z"))
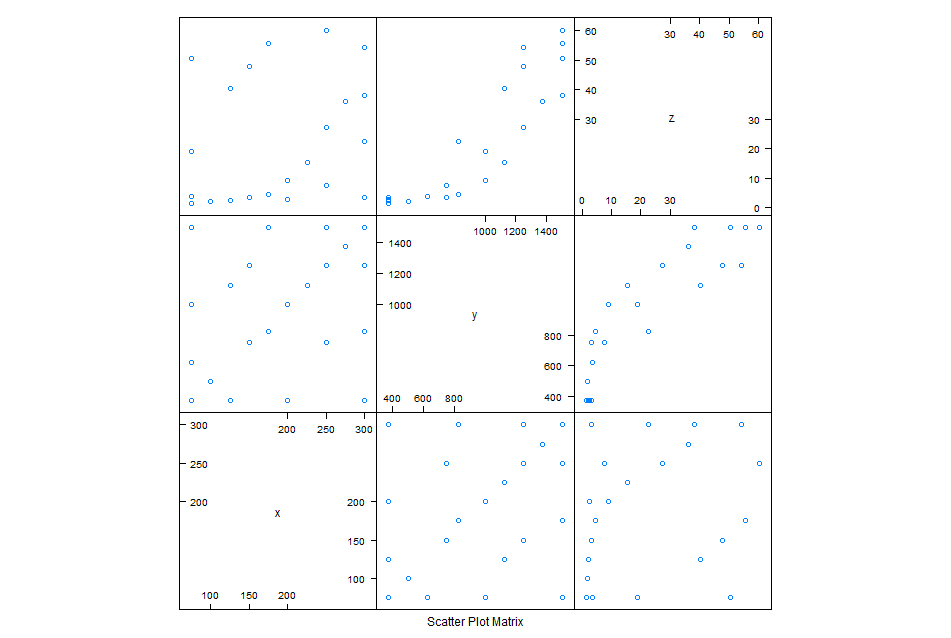
Кого-как, а меня не впечатлило. Икс у нас явно не при делах, а Игрек на линейную модель никак не тянет. Напрашивается экспонента. Проверим эту нехитрую мысль.
Введем фиктивную переменную lnZ равную натуральному логарифму от Z. В R это делается так.
Код:
> myData$lnZ<-log(myData$z)
> splom(~myData[,c("x","y","lnZ")],cex.labels=1.2,varnames=c("x","y","ln(z)"),col="red")
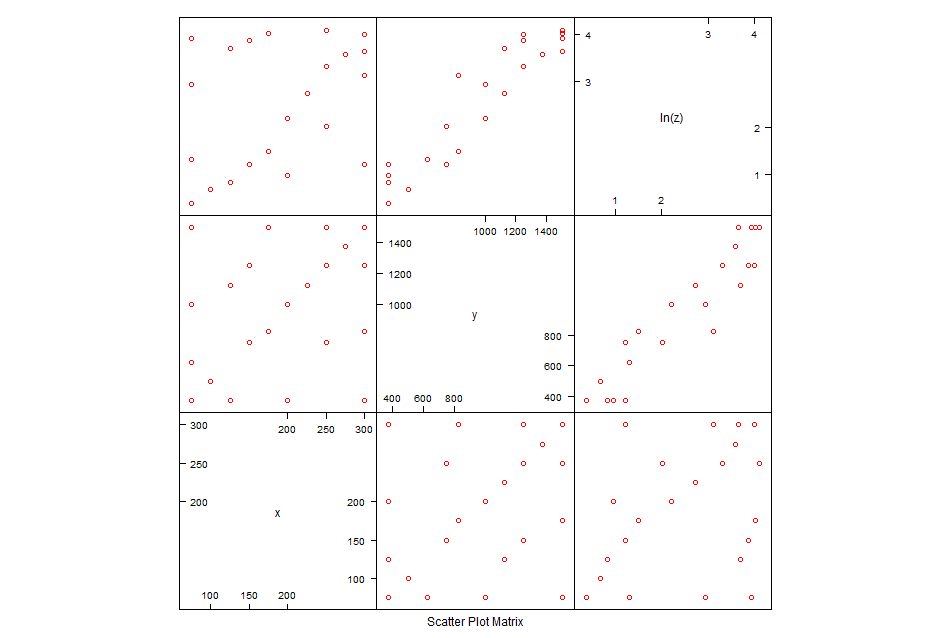
Поясняю, мы от модель вида  плавно перешли к  . В данном случае эпсилон у нас изображает остатки модели, которые, в идеальном варианте, должны иметь нормальное распределение.
Третий вариант мы можем получить логарифмированием всего и вся. В таком случае имеем 
Код:
> splom(~log(myData[,c("x","y","z")]),cex.labels=1.2,varnames=c("ln(x)","ln(y)","ln(z)"),col="dark green")
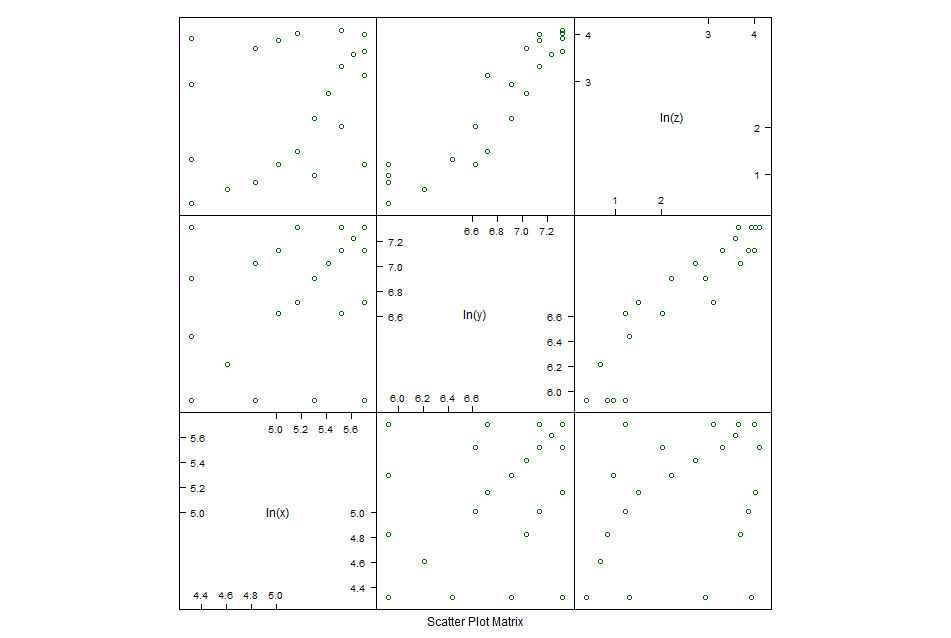
После такой работы уже можно и к моделированию переходить. Чисто чтоб поржать сделаем все три модели.
Код:
> summary(lm1<-lm(z~x+y))
Call:
lm(formula = z ~ x + y)
Residuals:
Min 1Q Median 3Q Max
-15.717 -8.306 1.616 6.760 17.840
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -21.233747 6.918102 -3.069 0.00631 **
x 0.001910 0.028261 0.068 0.94683
y 0.045646 0.005698 8.010 1.64e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 10.24 on 19 degrees of freedom
Multiple R-squared: 0.7846, Adjusted R-squared: 0.762
F-statistic: 34.61 on 2 and 19 DF, p-value: 4.624e-07
> summary(lm2<-lm(log(z)~x+y))
Call:
lm(formula = log(z) ~ x + y)
Residuals:
Min 1Q Median 3Q Max
-0.61700 -0.30351 -0.03218 0.19850 0.81873
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.5939071 0.3067107 -1.936 0.0678 .
x 0.0016541 0.0012529 1.320 0.2025
y 0.0029021 0.0002526 11.488 5.4e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4538 on 19 degrees of freedom
Multiple R-squared: 0.889, Adjusted R-squared: 0.8773
F-statistic: 76.08 on 2 and 19 DF, p-value: 8.53e-10
> summary(lm3<-lm(log(z)~log(x)+log(y)))
Call:
lm(formula = log(z) ~ log(x) + log(y))
Residuals:
Min 1Q Median 3Q Max
-0.9323 -0.2865 0.1118 0.3488 0.6532
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -14.5313 1.6847 -8.626 5.38e-08 ***
log(x) 0.2550 0.2275 1.121 0.276
log(y) 2.3263 0.2280 10.203 3.81e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5058 on 19 degrees of freedom
Multiple R-squared: 0.8621, Adjusted R-squared: 0.8476
F-statistic: 59.41 on 2 and 19 DF, p-value: 6.682e-09
Смотрим колонку Pr(>|t|) и количество звездочек сбоку. Начинаем модифицировать модель "a posteriori". Собственно говоря, Икс нам совершенно не нужен во всех его проявлениях. Непонятно зачем он вообще тут оказался. Возьмем вторую модель, она посимпатичнее и выкинем лишнее.
Код:
> summary(lm4<-lm(log(z)~y))
Call:
lm(formula = log(z) ~ y)
Residuals:
Min 1Q Median 3Q Max
-0.66190 -0.35391 -0.08276 0.28610 1.01267
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.3660607 0.2582089 -1.418 0.172
y 0.0029897 0.0002483 12.043 1.28e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4622 on 20 degrees of freedom
Multiple R-squared: 0.8788, Adjusted R-squared: 0.8727
F-statistic: 145 on 1 and 20 DF, p-value: 1.277e-10
Смотрим дальше. Свободный член (не радуйтесь девушки, это не то, что вы подумали) "Intercept" нам тоже не нужен. Да и пёс с ним.
Код:
> summary(lm5<-lm(log(z)~-1+y))
Call:
lm(formula = log(z) ~ -1 + y)
Residuals:
Min 1Q Median 3Q Max
-0.78397 -0.35742 -0.05766 0.18365 0.91500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
y 2.664e-03 9.699e-05 27.47 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4732 on 21 degrees of freedom
Multiple R-squared: 0.9729, Adjusted R-squared: 0.9716
F-statistic: 754.6 on 1 and 21 DF, p-value: < 2.2e-16
Обратите внимание какой у нас славный получился Эр квадрат. Дай бог всякому.
Моделька имеет вид 
Едем дальше. Впереди дисперсионный анализ.
Код:
> anova(lm5)
Analysis of Variance Table
Response: log(z)
Df Sum Sq Mean Sq F value Pr(>F)
y 1 168.946 168.946 754.61 < 2.2e-16 ***
Residuals 21 4.702 0.224
И графическое отображение остатков модели.
Код:
> par(mfrow=c(2,2))
> plot(lm5)
> par(mfrow=c(1,1))
Ну, лично мне нравится.

Итак, у нас есть модель и остатки. Если все хорошо, они должны иметь нормальное распределение с матожиданием 0. Судя по картинке (график квантилей) мы должны получить неплохой результат в тесте не нормальность распределения остатков модели.
Делаем тест Шапиро-Уилка. Смотрим и балдеем.
Код:
> shapiro.test(lm5$residuals)
Shapiro-Wilk normality test
data: lm5$residuals
W = 0.9628, p-value = 0.5488
Раз все так здорово, находим стандартное отклонение.
Код:
> sd(lm5$residuals)
[1] 0.4700086
> summary(lm5$residuals)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.78400 -0.35740 -0.05766 -0.05331 0.18360 0.91500
Sapienti sat.
Понятно, что в форумной заметке нельзя рассказать весь курс, но основные идеи я, надеюсь, рассказал.
P.S. Вот тут спрашивают, а как нарисовать 3D-график этого безобразия. Отвечаю. Просто. Например, так.
Код:
> library(scatterplot3d)
> scatterplot3d(x , y, z,highlight.3d=T,main="Вот такой график")

Последний раз редактировалось Hogfather; 05.12.2012 в 20:20.
|