Цитата:
Сообщение от Paul Kellerman
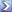
Имеется два населенных пункта: A и B, связанных небольшой транспортной сетью
с 8 мостами. Схема дорог и мостов показана на рисунке. Мосты считать абсолютно
одинаковыми, а также независимыми и одновременно введенными в эксплуатацию.
Мосты изнашиваются и никто их не ремонтирует. Время выхода из строя отдельного
моста есть случайная величина T распределенная по экспоненциальному закону, то
есть F(t) = 1 - exp(-t/tau), где параметр tau ожидаемый срок выхода моста из строя.
Ожидаемый срок - это по сути есть математическое ожидание случайной величины T.
Определить ожидаемый срок, когда будет невозможно доехать из пункта A в пункт B,
если ожидаемый срок выхода из строя для отдельного моста составляет tau = 30 лет.
|
Итак решение. Для возможности представления в виде графа и обработки на компьютере,
обозначим города как вершины с номерами 1 и 2, а мосты пронумеруем 3 - 10. Ниже приве-
ден поясняющий рисунок (мосты зеленые кружочки, города - красный и синий кружочки).

А далее смотрим pdf-файл. Короче ответ = 3/5 * tau = 18 лет.